Difference between revisions of "Special Considerations in Control Selection"
Bosmana fem (talk | contribs) (Created page with " Category:Choosing a Reference Group") |
Bosmana fem (talk | contribs) m |
||
| Line 1: | Line 1: | ||
| + | Controls in different types of case control studies: case cohort, traditional case control, density case control. Lets come back to the one of the characteristics of the control population, that they should be representative of exposures in the source population. In selecting controls for a case cohort study, a random sample of the source population should, if done correctly, be representative of the exposure distribution in the population that gives rise to the cases. In a traditional case control study, where cases are excluded from the control selection, a bias has been introduced as the exposure distribution in potential controls is no longer representative of the source population. If the attack rate is low, this bias will also be low, but if attack rate is high, the potential for bias will also be high. In a density case control study where cases occur over a long time period, controls should be selected from the source population still free of disease at the time the case occurs. In this way they should be representative of the person time experience of the source population [1] . | ||
| + | Asymptomatic cases. Does failure to identify those with mild or asymptomatic infection as cases introduce bias? This situation is analogous to non- response among cases. If the exposures among symptomatic and asymptomatic cases are the same, then no bias is introduced. There is only a reduction in statistical power. There is no difference in control selection if the controls are representative of the source population. | ||
| + | |||
| + | Example: In a hypothetical case control study with 40 cases and 40 controls, and 50% exposure among cases, Odds Ratio = 600/ 200 = 3.0 | ||
| + | |||
| + | {| class="wikitable" style="vertical-align:bottom;" | ||
| + | |- | ||
| + | ! | ||
| + | ! Cases | ||
| + | ! Controls | ||
| + | |- | ||
| + | | Exposed | ||
| + | | 20 | ||
| + | | 10 | ||
| + | |- | ||
| + | | Not exposed | ||
| + | | 20 | ||
| + | | 30 | ||
| + | |} | ||
| + | |||
| + | If we only detect 20 cases with the same number of controls , the Odds Ratio is unchanged (300/100 = 3.0) as long as % exposure is the same in detected and undetected cases. | ||
| + | |||
| + | {| class="wikitable" style="vertical-align:bottom;" | ||
| + | |- | ||
| + | ! | ||
| + | ! Cases | ||
| + | ! Controls | ||
| + | |- | ||
| + | | Exposed | ||
| + | | 10 | ||
| + | | 10 | ||
| + | |- | ||
| + | | Not exposed | ||
| + | | 10 | ||
| + | | 30 | ||
| + | |} | ||
| + | |||
| + | Immune subjects. If some of the population are immune at the start of the study, then they are not eligible to be cases. They should then also be excluded as controls as they are not part of the source population. In practice we do not usually know who is immune. Again this may not matter if % exposed is the same in immune and non-immune cases. However it may be that subjects are immune because they have already been cases in the past and that they have a similar level of exposure to the risk factor that caused the cases in the outbreak under study . This introduces bias that reduces the OR towards 1 and may result in a failure to detect a true association, especially if the proportion immune is high. For example, the inclusion of immune subjects in the control group is thought to explain the results of some case control studies that fail to show an association between contaminated drinking water and cryptosporidiosis [2] . | ||
| + | |||
| + | [[File:6471.image002.gif-550x0.png|1200px|frameless|left]]<br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
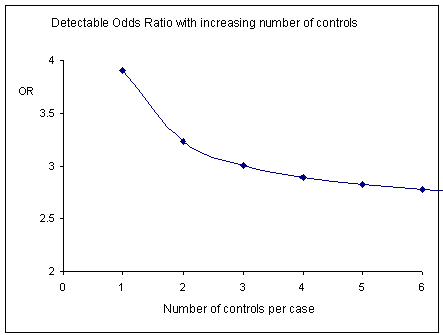
| + | Power and sample size in case control studies. A question often arises about the number of controls given a limited number of cases. Statistical programmes like Epi-Info can be used to estimate the sample size required to detect a specified odds ratio. It is unusual to select more than 3 or 4 controls per case as little statistical advantage is gained beyond this number (Figure) [3] . Alternatively we could show that power increases and plateaus with an increasing number of controls per case. The graph would then have the same shape but inverted. | ||
| + | |||
| + | =References= | ||
| + | 1. Rothmann KJ. Epidemiology: an introduction. Oxford University Press 2002. | ||
| + | |||
| + | 2. Hunter P. Modelling the impact of prior immunity, case misclassi®cation and bias on case-control studies in the investigation of outbreaks of cryptosporidiosis. Epidemiol Infect 2000;125:713-8. | ||
| + | |||
| + | 3. Kirkwood, B. R., Sterne, J.A.C. Essential Medical Statistics (2nd Ed). Blackwell Science 2003. | ||
| + | |||
| + | <div style="display: inline-block; width: 25%; vertical-align: top; border: 1px solid #000; background-color: #d7effc; padding: 10px; margin: 5px;"> | ||
| + | '''FEM PAGE CONTRIBUTORS 2007''' | ||
| + | ;Editor | ||
| + | :James Stuart | ||
| + | ;Original Authors | ||
| + | :Alain Moren | ||
| + | :James Stuart | ||
| + | ;Contributors | ||
| + | :sarika_desai | ||
| + | :Lisa Lazareck | ||
| + | :James Stuart | ||
| + | </div> | ||
[[Category:Choosing a Reference Group]] | [[Category:Choosing a Reference Group]] | ||
Revision as of 17:59, 11 April 2023
Controls in different types of case control studies: case cohort, traditional case control, density case control. Lets come back to the one of the characteristics of the control population, that they should be representative of exposures in the source population. In selecting controls for a case cohort study, a random sample of the source population should, if done correctly, be representative of the exposure distribution in the population that gives rise to the cases. In a traditional case control study, where cases are excluded from the control selection, a bias has been introduced as the exposure distribution in potential controls is no longer representative of the source population. If the attack rate is low, this bias will also be low, but if attack rate is high, the potential for bias will also be high. In a density case control study where cases occur over a long time period, controls should be selected from the source population still free of disease at the time the case occurs. In this way they should be representative of the person time experience of the source population [1] .
Asymptomatic cases. Does failure to identify those with mild or asymptomatic infection as cases introduce bias? This situation is analogous to non- response among cases. If the exposures among symptomatic and asymptomatic cases are the same, then no bias is introduced. There is only a reduction in statistical power. There is no difference in control selection if the controls are representative of the source population.
Example: In a hypothetical case control study with 40 cases and 40 controls, and 50% exposure among cases, Odds Ratio = 600/ 200 = 3.0
| Cases | Controls | |
|---|---|---|
| Exposed | 20 | 10 |
| Not exposed | 20 | 30 |
If we only detect 20 cases with the same number of controls , the Odds Ratio is unchanged (300/100 = 3.0) as long as % exposure is the same in detected and undetected cases.
| Cases | Controls | |
|---|---|---|
| Exposed | 10 | 10 |
| Not exposed | 10 | 30 |
Immune subjects. If some of the population are immune at the start of the study, then they are not eligible to be cases. They should then also be excluded as controls as they are not part of the source population. In practice we do not usually know who is immune. Again this may not matter if % exposed is the same in immune and non-immune cases. However it may be that subjects are immune because they have already been cases in the past and that they have a similar level of exposure to the risk factor that caused the cases in the outbreak under study . This introduces bias that reduces the OR towards 1 and may result in a failure to detect a true association, especially if the proportion immune is high. For example, the inclusion of immune subjects in the control group is thought to explain the results of some case control studies that fail to show an association between contaminated drinking water and cryptosporidiosis [2] .
Power and sample size in case control studies. A question often arises about the number of controls given a limited number of cases. Statistical programmes like Epi-Info can be used to estimate the sample size required to detect a specified odds ratio. It is unusual to select more than 3 or 4 controls per case as little statistical advantage is gained beyond this number (Figure) [3] . Alternatively we could show that power increases and plateaus with an increasing number of controls per case. The graph would then have the same shape but inverted.
References
1. Rothmann KJ. Epidemiology: an introduction. Oxford University Press 2002.
2. Hunter P. Modelling the impact of prior immunity, case misclassi®cation and bias on case-control studies in the investigation of outbreaks of cryptosporidiosis. Epidemiol Infect 2000;125:713-8.
3. Kirkwood, B. R., Sterne, J.A.C. Essential Medical Statistics (2nd Ed). Blackwell Science 2003.
FEM PAGE CONTRIBUTORS 2007
- Editor
- James Stuart
- Original Authors
- Alain Moren
- James Stuart
- Contributors
- sarika_desai
- Lisa Lazareck
- James Stuart
Root > Assessing the burden of disease and risk assessment > Field Epidemiology > Methods in Field Epidemiology > Types of Study > Choosing a Reference Group