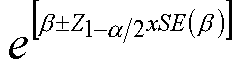Interpreting model coefficients: Difference between revisions
Bosmana fem (talk | contribs) |
Bosmana fem (talk | contribs) mNo edit summary |
||
| Line 357: | Line 357: | ||
The logit, including age as a continuous variable, is: | The logit, including age as a continuous variable, is: | ||
'''g(age) = - 0,6164 + ( 0,0001 x AGE)''' | '''g(age) = - 0,6164 + ( 0,0001 x AGE)''' | ||
For one year increase in age, the OR is multiplied by 1,0001, assuming linearity between age and log odds of gastroenteritis. For 10 years, an increase in the associated OR would be: | For one year increase in age, the OR is multiplied by 1,0001, assuming linearity between age and log odds of gastroenteritis. For 10 years, an increase in the associated OR would be: | ||
'''OR (10years) = exp (10 x 0,0001) = 2,72''' | '''OR (10years) = exp (10 x 0,0001) = 2,72''' | ||
Revision as of 20:07, 25 March 2023
The coefficients are the maximum likelihood estimates of β0 and β1. After fitting the model, the next step is interpreting those coefficients.
This time the question we need to answer is: "What do the estimates of the coefficients tell us about the research question?" For the logistic regression model, from the logit, which we will call g(x), we can write the following:
g(x) = β0+ β1x1 where β1 = g(x + 1) - g(x)
It is easy to understand that the coefficient β1 (the slope) represents the amount of change in the logit (g(x) for a change of one unit in the independent variable (x+1 versus x).
The interpretation of this change will depend upon the measurement scales used for the independent variable.
Dichotomous variable
First, let's assess what happens when the independent variable is dichotomous (e.g. yes, no). From the formula of the logit, Ln [( P(y/x) / (1-P(y/x)] = β0+ β1x1 we had deduced that the exponential of the coefficient (e β1) is the ratio of the odds of disease among exposed to the odds of disease among unexposed (see Logistic model).
β1= Ln (Odds ratio) e β1 = Odds ratio
In the case of a dichotomous variable, the odds ratio is the ratio of the odds for x = 1 to the odds of x = 0. The log of the odds ratio corresponds to the difference of the two logits with respectively x = 1 and x = 0. The odds ratio gives us an idea of how much more likely (or less likely) it is for the outcome (e.g. disease) to occur among those with x = 1 (e.g. exposed) as compared to those with x = 0 (e.g. unexposed).
The confidence interval around the odds ratio can be computed as follows:
The following example shows the results of a logistic regression analysis of a study done during the investigation of a Salmonella outbreak in which the consumption of Tiramisu was suspected to be the vehicle of the epidemic. The data set includes 245 individuals, including cases and controls.
| Number of terms | 2 | ||
|---|---|---|---|
| Total Number of Observations | 245 | ||
| Rejected as Invalid | 0 | ||
| Number of valid Observations | 245 | ||
| Summary Statistics | Value | DF | p=value |
| Deviance | 159,2489 | 243 | |
| Likelihood ratio test | 180,3927 | 2 | < 0.001 |
Parameter Estimates--------------------------------95% C.I
| Terms | Std.Error | p-value | Odds Ratio | Lower | Upper | |
|---|---|---|---|---|---|---|
| %GM | 0,3875 | < 0.001 | 0,0511 | 0,0239 | 0,1092 | |
| TIRA_ | 0,4586 | < 0.001 | 74,5578 | 30,3501 | 183,1579 | |
In this output, β0 = - 2,9741 and β1 = 4,3116
The related OR is, therefore, equal to eβ1 = e4,3116= 74,5578. It expresses that the odds of gastroenteritis are 74,5578 times higher among Tiramisu consumers than not.
The confidence interval, applying the above-mentioned formula, is [30,3501 - 183,1579].
Polytomous variable
The independent variable may have more than 2 categories. Let suppose that we want to assess the role of the amount of Tiramisu consumed in the outcome (gastroenteritis due to Salmonella) of the above example. In this example the independent variable has four categories (no consumption, small amount, medium and large). The categories are mutually exclusive. In the data set this variable was coded 0 for no consumption, 1 for small amount, 2 for medium and 3 for large amount. If an analysis is performed using this coding we obtain the following result.
| Number of valid Observations | 2 | ||
|---|---|---|---|
| Total Number of Observations | 245 | ||
| Rejected as Invalid | 0 | ||
| Number of valid Observations | 245 | ||
| Summary Statistics | Value | DF | p=value |
| Deviance | 161,3985 | 243 | |
| Likelihood ratio test | 178,2431 | 2 | < 0.001 |
Parameter Estimates---------------------------------------------------95% C.I
| Terms | Coefficient | Std.Error | p-value | Odds Ratio | Lower | Upper |
|---|---|---|---|---|---|---|
| %GM | -2,5463 | 0,3048 | < 0.001 | 0,0784 | 0,0431 | 0,1424 |
| TIRA_ | 2,8479 | 0,3440 | < 0.001 | 17,2518 | 8,7904 | 33,8580 |
In the above result, the T-portion coded as 0,1,2 or 3 is interpreted as a continuous variable. Under the assumption that the logit is linear in the continuous variable T-portion, the OR's value represents the amount the OR is multiplied by for each increase of one unit of T-portion.
In our example, when we go from no exposure to small (0 to 1) the OR is 17,2518. When the exposure increases from 1 to 2 (small to medium amount), the OR is also 17,2518. This means that moving from 0 to 2, the OR would be 17,2518 x 17,2518 = 297,62. Similarly, moving from 0 to 3 (no consumption versus large amount), the OR would be 17,25183 = 5134,56. This obviously does not represent the relation between dose and outcome. The values 0 to 3 have no numerical meaning. They are in fact, a code for categories.
In such a situation, we will create design variables (also called dummy variables or factor variables). The principle is that for n categories, we need to create n-1 design variables.
Using the example of the amount of Tiramisu, the three design variables (D1, D2 and D3) take the following values. For no consumption D1, D2 and D3 will be assigned a 0 value. For small amount D1 = 1 and D2 and D3 = 0. For average consumption D1 = 0, D2 = 1 and D3 = 0. For a large amount only D3 equals 1. This is summarised in the following table. The most frequent method is using a common reference group for coding design variables. Most logistic regression software packages will generate design variables using this method.
| Design (dummy) variables | |||
|---|---|---|---|
| Tiramisu consumption | D1 | D2 | D3 |
| None | 0 | 0 | 0 |
| Small | 1 | 0 | 0 |
| Medium | 0 | 1 | 0 |
| Large | 0 | 0 | 1 |
Using the design variables in the above example, we obtain the following result.
| Summary Statistics | Value | DF | p=value | |
|---|---|---|---|---|
| Deviance | 150,6160 | 241 | ||
| Likelihood ratio test | 189,0256 | 4 | < 0.001 |
Parameter Estimates------------------------------------------------95% C.I
| Terms | Coefficient | Std.Error | p-value | Odds Ratio | Lower | Upper |
|---|---|---|---|---|---|---|
| %GM | -2,9741 | 0,3875 | < 0.001 | 0,0511 | 0,0239 | 0,1092 |
| TPORTION2 ='1' | 3,7518 | 0,4858 | < 0.001 | 42,5966 | 16,4380 | 110,3828 |
| TPORTION2 ='2' | 5,3720 | 0,7168 | < 0.001 | 215,2858 | 52,8285 | 877,3287 |
| TPORTION2 ='3' | 5,2767 | 1,1181 | < 0.001 | 195,7142 | 21,8712 | 1751,3447 |
In the above table, the odds ratio for eating a small amount (as compared to no consumption) is 42,5966. The odds ratio for eating a medium amount as compared to no consumption is 215,2858; for large amounts, it is 195,7142 (similar to the OR for a medium portion). For the 3 categories the reference group is non consumers allowing therefore to compare odds ratios between categories of consumption.
Some important considerations on design variables merit to be noted:
All dummy variables should be considered as a single variable.
- Each dummy variable corresponds to a degree of freedom (important in modelling).
- Dummy variables can be created to indicate different levels of exposure (dose-response analysis).
- Dummy variables can be created to indicate different levels of a quantitative variable (especially when doubting about linearity, see below).
Continuous independent variable
Some of the variables we will include in logistic models are continuous (e.g. age in years, weight in grams, height in cm, etc.). In such a case the interpretation of the coefficient will depend upon the unit chosen for the independent variable and the assumption that the logit is continuous in the dependent variable.
The logit can be expressed as:
g(x) = β0+ β1x1
Here also, the coefficient β1 gives the amount of change in the log odds (logit) for each unit of change in the independent variable.
The following table illustrates the relationship between age and the occurrence of gastroenteritis due to Salmonella.
| Number of terms | 2 | ||
|---|---|---|---|
| Total Number of Observations | 245 | ||
| Rejected as Invalid | 6 | ||
| Number of valid Observations | 239 | ||
| Summary Statistics | Value | DF | p=value |
| Deviance | 309,9103 | 237 | |
| Likelihood ratio test | 21,4135 | 2 | < 0.001 |
Parameter Estimates------------------------------------------95% C.I
| Terms | Coefficient | Std.Error | p-value | Odds Ratio | Lower | Upper |
|---|---|---|---|---|---|---|
| %GM | -0,6164 | 0,2914 | 0,0344 | 0,5399 | 0,3050 | 0,9556 |
| AGE | 0,0001 | 0,0100 | 0,9882 | 1,0001 | 0,9808 | 1,0199 |
The logit, including age as a continuous variable, is:
g(age) = - 0,6164 + ( 0,0001 x AGE)
For one year increase in age, the OR is multiplied by 1,0001, assuming linearity between age and log odds of gastroenteritis. For 10 years, an increase in the associated OR would be:
OR (10years) = exp (10 x 0,0001) = 2,72
In the above example, age seems to slightly increase the risk of illness.
However, suppose the logit is not linear. In that case, we should choose another way of analysis, e.g. creating categories of age (age groups) and developing the related design (dummy) variables or using other regression analysis techniques.
FEM PAGE CONTRIBUTORS 2007
- Editor
- Fernando Simon
- Original Author
- Alain Moren
- Contributors
- Arnold Bosman
- Lisa Lazareck
- Fernando Simon