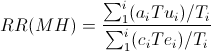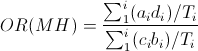Difference between revisions of "The Mantel Haenszel Method"

From
Jump to: navigation, search
m
m
 
Line 119: Line 119:
 
|}
 
|}
  
−
In our example the crude measure of effect (the risk ratio) was 4.5. The weighted measure of effect calculated with the Mantel Haenszel method is close to 1. It is obtained as follows:
+
In our example, the crude measure of effect (the risk ratio) was 4.5. The weighted measure of effect calculated with the Mantel Haenszel method is close to 1. It is obtained as follows:
 
[[File:MH-1.png|800px|frameless|center]]
 
[[File:MH-1.png|800px|frameless|center]]
  
Line 126: Line 126:
 
The relative difference between the weighted and the crude measures of effect is more than 15% (4.5/0.99 *100 = 450%) therefore suggesting that, in our hypothetical study, vaccination is confounding (is a confounding factor for) the association between gender and disease. Had a stratified analysis been omitted, the data may lead to the conclusion that being a boy was a risk factor for the disease.
 
The relative difference between the weighted and the crude measures of effect is more than 15% (4.5/0.99 *100 = 450%) therefore suggesting that, in our hypothetical study, vaccination is confounding (is a confounding factor for) the association between gender and disease. Had a stratified analysis been omitted, the data may lead to the conclusion that being a boy was a risk factor for the disease.
  
−
The adjusted RR 0.99 is presented, which concludes that this is the measure of association between gender and disease. This is different from effect modification, where two RRs would be presented.
+
The adjusted RR 0.99 is presented, which concludes that this is the measure of association between gender and disease. This differs from [[Effect Modification|effect modification]], where two RRs would be presented.
  
−
Mathematically, the adjusted estimate is a weighted average of the stratum specific measures of the risk ratio. It will therefore always lie within the range of the stratum specific measures of the effect. (i.e. in the example above;  0.99 is between the range 0.95 and 1.00 - the stratum specific RRs).
+
Mathematically, the adjusted estimate is a weighted average of the stratum-specific measures of the risk ratio. It will, therefore, always lie within the range of the stratum-specific measures of the effect. (i.e. in the example above;  0.99 is between the range 0.95 and 1.00 - the stratum-specific RRs).
 +
 
 +
For a case-control study, the Mantel Haenszel odds ratio (ORMH) can be computed as follows:
 +
 
 +
{| class="wikitable" style="font-style:italic; background-color:#FFF;"
 +
|- style="font-style:normal; font-weight:bold;"
 +
! Stratified
 +
! Risk Factor
 +
! Cases
 +
! Controls
 +
! Totals
 +
|-
 +
| rowspan="3" style="font-weight:bold; font-style:normal;" | Stratum 1
 +
| style="font-style:normal;" | Exposed
 +
| a1
 +
| b1
 +
|
 +
|-
 +
| style="font-style:normal;" | Unexposed
 +
| c1
 +
| d1
 +
|
 +
|-
 +
| style="font-style:normal;" |
 +
|
 +
|
 +
| T1
 +
|-
 +
| rowspan="3" style="font-weight:bold; font-style:normal;" | Stratum 2
 +
| style="font-style:normal;" | Exposed
 +
| a2
 +
| b2
 +
|
 +
|-
 +
| style="font-style:normal;" | Unexposed
 +
| c2
 +
| d2
 +
|
 +
|-
 +
| style="font-style:normal;" |
 +
|
 +
|
 +
| T2
 +
|}
 +
 
 +
[[File:1401.MH-OR.gif-550x0.png|800px|frameless|left]]
 +
 
 +
In which:
 +
a and c are the number of cases exposed and unexposed in a stratum,
 +
b and d are the number of controls exposed and unexposed in a stratum.
 +
T is the total for a stratum
 +
The sums ∑ are calculated for the i strata.
 +
 
 +
It can become customary to 'eyeball' the data: comparing the crude measure to the range of the stratum-specific measures. If the crude measure is not included in the range between stratum-specific measures, confounding may exist.
 +
 
 +
A watertight method for identifying confounding variables exists. It requires the construction of a causal diagram summarizing the knowledge and assumptions between all exposures, confounders and disease outcome, which is then analysed using graphical algorithms <Ref>Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology 1999 Jan;10(1):37-48.</ref>. 
 +
 
 +
 
 +
=References=
 +
<References/>
  
−
For a case control study the Mantel Haenszel odds ratio (ORMH) can be computed as follows:
 
  
  
 
[[Category:Stratified Analysis]]
 
[[Category:Stratified Analysis]]

Latest revision as of 20:53, 25 March 2023

The most popular method used to compute a weighted risk ratio or odds ratio is the Mantel-Haenszel method, which can be used for risk ratios or rate ratios.

From the following table

Cases Total
Stratum 1 Exposed a1 Te1
Unexposed c1 Tu1
Total T1
Stratum 2 Exposed a2 Te2
Unexposed c2 Tu2
Total T2

The Mantel Haenszel risk ratio (RRMH) can be computed as follows:

8206.MH-RR.gif-550x0.png

In which: a and c are the number of cases exposed and unexposed in a stratum Te and Tu are the total number exposed and unexposed in a stratum T is the total of a stratum The sums ∑ are calculated for the i strata.

Returning to the example of the cohort study with vaccinated girls and boys:

Crude RR

Gender Cases Total Attack Rate RR
Boys 819 1000 82% 4.52
Girls 181 1000 18% ref

Stratified RRs

Gender Cases Total Attack Rate RR
Unvaccinated Boys 814 950 86% 1.00
Girls 86 100 86% ref
1050
Vaccinated Boys 5 50 10% 0.95
Girls 95 900 11% ref
950

In our example, the crude measure of effect (the risk ratio) was 4.5. The weighted measure of effect calculated with the Mantel Haenszel method is close to 1. It is obtained as follows:

MH-1.png


The relative difference between the weighted and the crude measures of effect is more than 15% (4.5/0.99 *100 = 450%) therefore suggesting that, in our hypothetical study, vaccination is confounding (is a confounding factor for) the association between gender and disease. Had a stratified analysis been omitted, the data may lead to the conclusion that being a boy was a risk factor for the disease.

The adjusted RR 0.99 is presented, which concludes that this is the measure of association between gender and disease. This differs from effect modification, where two RRs would be presented.

Mathematically, the adjusted estimate is a weighted average of the stratum-specific measures of the risk ratio. It will, therefore, always lie within the range of the stratum-specific measures of the effect. (i.e. in the example above; 0.99 is between the range 0.95 and 1.00 - the stratum-specific RRs).

For a case-control study, the Mantel Haenszel odds ratio (ORMH) can be computed as follows:

Stratified Risk Factor Cases Controls Totals
Stratum 1 Exposed a1 b1
Unexposed c1 d1
T1
Stratum 2 Exposed a2 b2
Unexposed c2 d2
T2
1401.MH-OR.gif-550x0.png

In which: a and c are the number of cases exposed and unexposed in a stratum, b and d are the number of controls exposed and unexposed in a stratum. T is the total for a stratum The sums ∑ are calculated for the i strata.

It can become customary to 'eyeball' the data: comparing the crude measure to the range of the stratum-specific measures. If the crude measure is not included in the range between stratum-specific measures, confounding may exist.

A watertight method for identifying confounding variables exists. It requires the construction of a causal diagram summarizing the knowledge and assumptions between all exposures, confounders and disease outcome, which is then analysed using graphical algorithms [1].


References

  1. ↑ Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology 1999 Jan;10(1):37-48.
Retrieved from "https://femwiki.org/index.php?title=The_Mantel_Haenszel_Method&oldid=1167"

Contributors