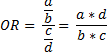Difference between revisions of "Category:Odds"
Bosmana fem (talk | contribs) m |
Bosmana fem (talk | contribs) m (Bosmana fem moved page Odds to Category:Odds) |
||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | =Absolute Number= | ||
Odds (no synonyms), are expressed as an absolute number. | Odds (no synonyms), are expressed as an absolute number. | ||
| − | The odds of an event ("odds", always plural) occurring is the probability (e.g. risk) that this event will occur divided by the probability that the event will not occur. It can also be expressed as the probability that an event will occur divided by "1 minus the probability that the event will occur"<ref>Porta, M. A | + | The odds of an event ("odds", always plural) occurring is the probability (e.g. risk) that this event will occur divided by the probability that the event will not occur. It can also be expressed as the probability that an event will occur divided by "1 minus the probability that the event will occur"<ref>Porta, M. A Dictionary of Epidemiology, Fifth edition. Oxford University press, 2008.</ref>. |
P | P | ||
| Line 7: | Line 8: | ||
1 - P | 1 - P | ||
| − | This probability measure is popular in the world of gambling. If we compute the number of people putting money on one horse winning and the number of people putting money on the horse not winning (i.e. putting money on other horses) we can compute the odds of winning. For example among 3100 persons gambling on horses, 100 persons put money on horse "A" to win and 3000 do not (they bet on other horses). The odds of winning are then 1/30 (100/3100 divided by 3000/3100 which can be simplified as 100/3000 or 1 / 30). In fact in gambling the odds of not winning are preferred and expressed as a ratio X/1. In our example, 30/1, or in words "thirty to one". This means that for every Euro that you bet, you will receive 30 if you win. | + | This probability measure is popular in the world of gambling. If we compute the number of people putting money on one horse winning and the number of people putting money on the horse not winning (i.e., putting money on other horses), we can compute the odds of winning. For example, among 3100 persons gambling on horses, 100 persons put money on horse "A" to win, and 3000 do not (they bet on other horses). The odds of winning are then 1/30 (100/3100 divided by 3000/3100 which can be simplified as 100/3000 or 1 / 30). In fact, in gambling, the odds of not winning are preferred and expressed as a ratio X/1. In our example, 30/1, or in words, "thirty to one". This means that for every Euro that you bet, you will receive 30 if you win. |
| − | Since | + | Since we illustrate the population under investigation in epidemiology with a two-by-two table, we will use a table to describe how to calculate odds. In the two-by-two table, the concept of exposure is also included. However, to calculate the odds of disease, it is not necessary to consider that in our population, some might have been exposed to a particular exposure and some not. |
| − | Example 1 | + | ===Example 1=== |
{| class="wikitable" | {| class="wikitable" | ||
| − | ! Developing the disease !! Not developing the disease !! Total | + | ! !! Developing the disease !! Not developing the disease !! Total |
|- | |- | ||
| Exposed || a || b || a+b | | Exposed || a || b || a+b | ||
| Line 24: | Line 25: | ||
[[File:0028.risk of dis.png-550x0.png|400px|frameless|left]] | [[File:0028.risk of dis.png-550x0.png|400px|frameless|left]] | ||
| − | [[File:2086.odds of dis.png-550x0.png| | + | [[File:2086.odds of dis.png-550x0.png|600px|frameless|left]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Therefore to calculate the odds: divide the risk of getting the disease by the risk of not getting the disease. It is equal to the ratio of the number of people with the disease to the number of people without it in a particular population. | Therefore to calculate the odds: divide the risk of getting the disease by the risk of not getting the disease. It is equal to the ratio of the number of people with the disease to the number of people without it in a particular population. | ||
| Line 38: | Line 46: | ||
Disease-odds ratio: | Disease-odds ratio: | ||
[[File:2330.or simple.png-550x0.png|400px|frameless|left]] | [[File:2330.or simple.png-550x0.png|400px|frameless|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 44: | Line 56: | ||
For this reason, in many situations (when the disease is rare) the odds ratio can estimate the risk ratio. | For this reason, in many situations (when the disease is rare) the odds ratio can estimate the risk ratio. | ||
| − | Example 2 | + | ===Example 2=== |
{| class="wikitable" | {| class="wikitable" | ||
| − | ! Developing the disease !! Not developing the disease !! Total | + | ! !! Developing the disease !! Not developing the disease !! Total |
|- | |- | ||
| Exposed || a || b || a+b | | Exposed || a || b || a+b | ||
| Line 59: | Line 71: | ||
Odds of disease (50 / 100000) / 1 - (50/100000) = 0.00050025 | Odds of disease (50 / 100000) / 1 - (50/100000) = 0.00050025 | ||
| − | |||
| − | Example 3 | + | When getting the disease is rare, the risk of disease approximates the odds of disease. |
| + | |||
| + | ===Example 3=== | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | ! Developing the disease !! Not developing the disease !! Total | + | ! !! Developing the disease !! Not developing the disease !! Total |
|- | |- | ||
| Exposed || a || b || a+b | | Exposed || a || b || a+b | ||
| Line 73: | Line 86: | ||
|} | |} | ||
| − | Risk of disease = 50 / 1000 | + | Risk of disease = 50 / 1000 = 0.05000 |
| + | |||
Odds of disease (50 / 1000) / 1 - (50/1000) = 0.05263 | Odds of disease (50 / 1000) / 1 - (50/1000) = 0.05263 | ||
| Line 80: | Line 94: | ||
=Credits= | =Credits= | ||
| + | ===FEM Editor 2007=== | ||
| + | * Sabrina Bacci | ||
| + | ===Original Authors=== | ||
| + | * Alain Moren | ||
| + | * Marta Valenciano | ||
| + | * Arnold Bosman | ||
| + | ===FEM Contributors=== | ||
| + | * Arnold Bosman | ||
| + | * Naomi Boxall | ||
| + | * Vladimir Prikazsky | ||
| + | * Aileen Kitching | ||
| + | * Lisa Lazareck | ||
| + | * Sabrina Bacci | ||
| + | |||
| + | |||
| + | [[Category:Measures of Disease Occurrence]] | ||
Latest revision as of 21:14, 22 March 2023
Contents
Absolute Number
Odds (no synonyms), are expressed as an absolute number.
The odds of an event ("odds", always plural) occurring is the probability (e.g. risk) that this event will occur divided by the probability that the event will not occur. It can also be expressed as the probability that an event will occur divided by "1 minus the probability that the event will occur"[1].
P
Odds of event = -----------
1 - P
This probability measure is popular in the world of gambling. If we compute the number of people putting money on one horse winning and the number of people putting money on the horse not winning (i.e., putting money on other horses), we can compute the odds of winning. For example, among 3100 persons gambling on horses, 100 persons put money on horse "A" to win, and 3000 do not (they bet on other horses). The odds of winning are then 1/30 (100/3100 divided by 3000/3100 which can be simplified as 100/3000 or 1 / 30). In fact, in gambling, the odds of not winning are preferred and expressed as a ratio X/1. In our example, 30/1, or in words, "thirty to one". This means that for every Euro that you bet, you will receive 30 if you win.
Since we illustrate the population under investigation in epidemiology with a two-by-two table, we will use a table to describe how to calculate odds. In the two-by-two table, the concept of exposure is also included. However, to calculate the odds of disease, it is not necessary to consider that in our population, some might have been exposed to a particular exposure and some not.
Example 1
| Developing the disease | Not developing the disease | Total | |
|---|---|---|---|
| Exposed | a | b | a+b |
| Not exposed | c | d | c+d |
| Total | 30 | 70 | 100 |
The table yields the following calculations:
Therefore to calculate the odds: divide the risk of getting the disease by the risk of not getting the disease. It is equal to the ratio of the number of people with the disease to the number of people without it in a particular population.
The odds is a measure rarely used in epidemiology. Most often the odds are used to express the odds ratio. A disease-odds ratio is the ratio of the odds of having the disease among the exposed and the odds of having the disease among the unexposed [1]. In other words, the odds ratio is the ratio of the odds of disease observed in 2 subsets of a population.
In you take again the table as an example, the disease-odds ratio will be equal to:
Odds of developing the disease among the exposed: a / b
Odds of developing the disease among the unexposed: c / d
Disease-odds ratio:
As you see by comparing example one, two and three, the risk and the odds approximate each other when the event is rare. When the event occurs frequently the odds overestimate the risk of disease.
For this reason, in many situations (when the disease is rare) the odds ratio can estimate the risk ratio.
Example 2
| Developing the disease | Not developing the disease | Total | |
|---|---|---|---|
| Exposed | a | b | a+b |
| Not exposed | c | d | c+d |
| Total | 50 | 99 950 | 100 000 |
Risk of disease = 50 / 100000 = 0.00050000
Odds of disease (50 / 100000) / 1 - (50/100000) = 0.00050025
When getting the disease is rare, the risk of disease approximates the odds of disease.
Example 3
| Developing the disease | Not developing the disease | Total | |
|---|---|---|---|
| Exposed | a | b | a+b |
| Not exposed | c | d | c+d |
| Total | 59 | 950 | 1000 |
Risk of disease = 50 / 1000 = 0.05000
Odds of disease (50 / 1000) / 1 - (50/1000) = 0.05263
References
- ↑ Porta, M. A Dictionary of Epidemiology, Fifth edition. Oxford University press, 2008.
Credits
FEM Editor 2007
- Sabrina Bacci
Original Authors
- Alain Moren
- Marta Valenciano
- Arnold Bosman
FEM Contributors
- Arnold Bosman
- Naomi Boxall
- Vladimir Prikazsky
- Aileen Kitching
- Lisa Lazareck
- Sabrina Bacci