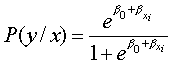Category:Fitting logistic regression models: Difference between revisions
Bosmana fem (talk | contribs) mNo edit summary |
Bosmana fem (talk | contribs) mNo edit summary |
||
| Line 1: | Line 1: | ||
Once we have a model (the logistic regression model), we need to fit it to a set of data to estimate the parameters β0 and β1. | Once we have a model ([[The logistic model|the logistic regression model]]), we need to fit it to a set of data to estimate the parameters β0 and β1. | ||
In linear regression, we mentioned that the straight line fitting the data could be obtained by minimizing the distance between each dot of a plot and the regression line. In fact, we minimize the sum of the squares of the distance between dots and the regression line (squared to avoid negative differences). This is called the least sum of squares method. We identify b0 and b, which minimise the sum of squares. | In linear regression, we mentioned that the straight line fitting the data could be obtained by minimizing the distance between each dot of a plot and the regression line. In fact, we minimize the sum of the squares of the distance between dots and the regression line (squared to avoid negative differences). This is called the least sum of squares method. We identify b0 and b, which minimise the sum of squares. | ||
In logistic regression, the method is more complicated. It is called the maximum likelihood method. The maximum likelihood will provide values of β0 and β1 which maximise the probability of obtaining the data set. It requires iterative computing and is easily done with most computer software. | |||
We use the likelihood function to estimate the probability of observing the data, given the unknown parameters (β0 and βb1). A "likelihood" is a probability, specifically the probability that the observed values of the dependent variable may be predicted from the observed values of the independent variables. Like any probability, the likelihood varies from 0 to 1. | We use the likelihood function to estimate the probability of observing the data, given the unknown parameters (β0 and βb1). A "likelihood" is a probability, specifically the probability that the observed values of the dependent variable may be predicted from the observed values of the independent variables. Like any probability, the likelihood varies from 0 to 1. | ||
| Line 10: | Line 10: | ||
The log-likelihood is defined as: | The log-likelihood is defined as: | ||
[[File:3060.image015.gif-550x0.png| | [[File:3060.image015.gif-550x0.png|800px|frameless|center]] | ||
In which | In which | ||
[[File:5074.probY.gif-550x0.png| | [[File:5074.probY.gif-550x0.png|800px|frameless|center]] | ||
Estimating the parameters β0 and β1 is done using the first derivatives of log-likelihood (these are called the likelihood equations), and solving them for β0 and β1. Iterative computing is used. An arbitrary value for the coefficients (usually 0) is first chosen. Then log-likelihood is computed and variation of coefficients values observed. Reiteration is then performed until maximisation (plateau). The results are the maximum likelihood estimates of β0 and β1. | Estimating the parameters β0 and β1 is done using the first derivatives of log-likelihood (these are called the likelihood equations), and solving them for β0 and β1. Iterative computing is used. An arbitrary value for the coefficients (usually 0) is first chosen. Then log-likelihood is computed and variation of coefficients values observed. Reiteration is then performed until maximisation (plateau). The results are the maximum likelihood estimates of β0 and β1. | ||
Inference testing | =Inference testing= | ||
Now that we have estimates for β0 and β1, the next step is inference testing. | Now that we have estimates for β0 and β1, the next step is inference testing. | ||
It responds to the question: "Does the model including a given independent variable provide more information about occurrence of disease than the model without this variable?" The response is obtained by comparing the observed values of the dependent variable to values predicted by two models, one with the independent variable of interest and one without. If the predicted values | It responds to the question: "'''Does the model including a given independent variable provide more information about the occurrence of disease than the model without this variable?'''" The response is obtained by comparing the observed values of the dependent variable to values predicted by two models, one with the independent variable of interest and one without. If the model's predicted values with the independent variable are better, then this variable significantly contributes to the outcome. To do so, we will use a statistical test. | ||
Three tests are frequently used: | Three tests are frequently used: | ||
* Likelihood ratio statistic (LRS) | |||
* Wald test | |||
* Score test | |||
The Likelihood ratio statistic (LRS) can be directly computed from the likelihood functions of both models. | |||
- | Probabilities are always less than one, so log-likelihoods are always negative; we then work with negative log-likelihoods for convenience. | ||
The | The likelihood ratio statistic (LRS) is a test of the significance of the difference (the ratio is expressed in log) between the likelihood for the researcher's model minus the likelihood for a reduced model (the models with and without a given variable). | ||
The LRS can be used to test the significance of a full model (several independent variables in the model versus no variable = only the constant). In that situation, it tests the probability (the null hypothesis) that all β are equal to 0 (all slopes corresponding to each variable are equal to 0). This implies that none of the independent variables is linearly related to the log odds of the dependent variable. | |||
The LRS does not tell us if a particular independent variable is more important than others. This can be done, however, by comparing the likelihood of the overall model with a reduced model, which drops one of the independent variables. | |||
In that case, the LRS tests if the logistic regression coefficient for the dropped variable equals 0. If so it would justify dropping the variable from the model. A non-significant LRS indicates no difference between the full and the reduced models. | |||
Alternatively, LRS can be computed from deviances. | |||
Computations from deviances | Computations from deviances | ||
| Line 54: | Line 48: | ||
In which D- and D+ are respectively the deviances of the models without and with the variable of interest. | In which D- and D+ are, respectively the deviances of the models without and with the variable of interest. | ||
The deviance can be computed as follows: | The deviance can be computed as follows: | ||
| Line 62: | Line 56: | ||
(A saturated model | (A saturated model is a model in which there are as many parameters as data points.) | ||
| Line 105: | Line 99: | ||
{| class="wikitable" style="text-align:right; vertical-align:bottom;" | |||
|- | |||
! Terms | |||
! Coefficient | |||
! Std.Error | |||
! p-value | |||
! Odds Ratio | |||
Terms | ! Lower | ||
! Upper | |||
Coefficient | |- | ||
| %GM | |||
Std.Error | | -17,457 | ||
| 0,1782 | |||
p-value | | < 0.001 | ||
| 0,1745 | |||
Odds Ratio | | 0,1231 | ||
| 0,2475 | |||
Lower | |- | ||
| OC | |||
Upper | | 19,868 | ||
| 0,2281 | |||
%GM | | < 0.001 | ||
| 72,924 | |||
- | | 46,633 | ||
| 114,037 | |||
0,1782 | |} | ||
< 0.001 | |||
0,1745 | |||
0,1231 | |||
0,2475 | |||
OC | |||
0,2281 | |||
< 0.001 | |||
In model 2, model 1 was expended and another variable was added (the age in years). Here again the addition of the second variable contributes significantly to the model. The LRS (LRS = 16,7253, p < 0,001) expresses the difference in likelihood between the two models. | In model 2, model 1 was expended and another variable was added (the age in years). Here again the addition of the second variable contributes significantly to the model. The LRS (LRS = 16,7253, p < 0,001) expresses the difference in likelihood between the two models. | ||
| Line 199: | Line 171: | ||
{| class="wikitable" style="background-color:#FFF;" | |||
|- | |||
! Terms | |||
! Coefficient | |||
! Std.Error | |||
Terms | ! p-value | ||
! Odds Ratio | |||
Coefficient | ! Lower | ||
! Upper | |||
Std.Error | |- | ||
| %GM | |||
p-value | | style="background-color:#FF9;" | -3,3191 | ||
| 0,4511 | |||
Odds Ratio | | < 0.001 | ||
| 0,0362 | |||
Lower | | 0,0149 | ||
| 0,0876 | |||
Upper | |- | ||
| OC | |||
%GM | | style="background-color:#FF9;" | 2,3294 | ||
| 0,2573 | |||
-3,3191 | | < 0.001 | ||
| 10,2717 | |||
0,4511 | | 6,2032 | ||
| 17,0086 | |||
< 0.001 | |- | ||
| AGE | |||
0,0362 | | style="background-color:#FF9;" | 0,0302 | ||
| 0,0075 | |||
0,0149 | | < 0.001 | ||
| 1,0306 | |||
0,0876 | | 1,0156 | ||
| 1,0459 | |||
OC | |} | ||
2,3294 | |||
0,2573 | |||
< 0.001 | |||
10,2717 | |||
6,2032 | |||
17,0086 | |||
AGE | |||
0,0302 | |||
0,0075 | |||
< 0.001 | |||
1,0306 | |||
1,0156 | |||
1,0459 | |||
[[Category:Logistic Regression]] | [[Category:Logistic Regression]] | ||
Revision as of 19:21, 25 March 2023
Once we have a model (the logistic regression model), we need to fit it to a set of data to estimate the parameters β0 and β1.
In linear regression, we mentioned that the straight line fitting the data could be obtained by minimizing the distance between each dot of a plot and the regression line. In fact, we minimize the sum of the squares of the distance between dots and the regression line (squared to avoid negative differences). This is called the least sum of squares method. We identify b0 and b, which minimise the sum of squares.
In logistic regression, the method is more complicated. It is called the maximum likelihood method. The maximum likelihood will provide values of β0 and β1 which maximise the probability of obtaining the data set. It requires iterative computing and is easily done with most computer software.
We use the likelihood function to estimate the probability of observing the data, given the unknown parameters (β0 and βb1). A "likelihood" is a probability, specifically the probability that the observed values of the dependent variable may be predicted from the observed values of the independent variables. Like any probability, the likelihood varies from 0 to 1.
Practically, it is easier to work with the logarithm of the likelihood function. This function is known as the log-likelihood and will be used for inference testing when comparing several models. The log-likelihood varies from 0 to minus infinity (it is negative because the natural log of any number less than 1 is negative).
The log-likelihood is defined as:
In which
Estimating the parameters β0 and β1 is done using the first derivatives of log-likelihood (these are called the likelihood equations), and solving them for β0 and β1. Iterative computing is used. An arbitrary value for the coefficients (usually 0) is first chosen. Then log-likelihood is computed and variation of coefficients values observed. Reiteration is then performed until maximisation (plateau). The results are the maximum likelihood estimates of β0 and β1.
Inference testing
Now that we have estimates for β0 and β1, the next step is inference testing.
It responds to the question: "Does the model including a given independent variable provide more information about the occurrence of disease than the model without this variable?" The response is obtained by comparing the observed values of the dependent variable to values predicted by two models, one with the independent variable of interest and one without. If the model's predicted values with the independent variable are better, then this variable significantly contributes to the outcome. To do so, we will use a statistical test.
Three tests are frequently used:
- Likelihood ratio statistic (LRS)
- Wald test
- Score test
The Likelihood ratio statistic (LRS) can be directly computed from the likelihood functions of both models.
Probabilities are always less than one, so log-likelihoods are always negative; we then work with negative log-likelihoods for convenience.
The likelihood ratio statistic (LRS) is a test of the significance of the difference (the ratio is expressed in log) between the likelihood for the researcher's model minus the likelihood for a reduced model (the models with and without a given variable).
The LRS can be used to test the significance of a full model (several independent variables in the model versus no variable = only the constant). In that situation, it tests the probability (the null hypothesis) that all β are equal to 0 (all slopes corresponding to each variable are equal to 0). This implies that none of the independent variables is linearly related to the log odds of the dependent variable.
The LRS does not tell us if a particular independent variable is more important than others. This can be done, however, by comparing the likelihood of the overall model with a reduced model, which drops one of the independent variables.
In that case, the LRS tests if the logistic regression coefficient for the dropped variable equals 0. If so it would justify dropping the variable from the model. A non-significant LRS indicates no difference between the full and the reduced models.
Alternatively, LRS can be computed from deviances.
Computations from deviances
In which D- and D+ are, respectively the deviances of the models without and with the variable of interest.
The deviance can be computed as follows:
(A saturated model is a model in which there are as many parameters as data points.)
Under the hypothesis that β1= 0, LRS follows a chi-square distribution with 1 degree of freedom. The derived p-value can be computed.
The following table illustrates the result of the analysis (using a logistic regression package) of a study assessing risk factors for myocardial infarction. The LRS equals 138,7821 (p < 0,001) suggesting that oral contraceptive (OC) use is a significant predictor of the outcome.
Table 1: Risk factors for myocardial infarction. Logistic regression model including a single independent variable (OC)
Number of valid Observations
449
Model Fit Results
Value
DF
p-value
Likelihood ratio statistic
138,7821
2
< 0.001
Parameter Estimates
| Terms | Coefficient | Std.Error | p-value | Odds Ratio | Lower | Upper |
|---|---|---|---|---|---|---|
| %GM | -17,457 | 0,1782 | < 0.001 | 0,1745 | 0,1231 | 0,2475 |
| OC | 19,868 | 0,2281 | < 0.001 | 72,924 | 46,633 | 114,037 |
In model 2, model 1 was expended and another variable was added (the age in years). Here again the addition of the second variable contributes significantly to the model. The LRS (LRS = 16,7253, p < 0,001) expresses the difference in likelihood between the two models.
Table 2: Risk factors for myocardial infarction. Logistic regression model including two independent variable (OC and AGE)
Number of valid Observations
449
Model Fit Results
Value
DF
p-value
Likelihood ratio statistic
16,7253
1
< 0.001
Parameter Estimates
| Terms | Coefficient | Std.Error | p-value | Odds Ratio | Lower | Upper |
|---|---|---|---|---|---|---|
| %GM | -3,3191 | 0,4511 | < 0.001 | 0,0362 | 0,0149 | 0,0876 |
| OC | 2,3294 | 0,2573 | < 0.001 | 10,2717 | 6,2032 | 17,0086 |
| AGE | 0,0302 | 0,0075 | < 0.001 | 1,0306 | 1,0156 | 1,0459 |
Pages in category "Fitting logistic regression models"
The following 2 pages are in this category, out of 2 total.